Veri Bilimcinin İstatistik El Kitabı
Merhabalar bu yazımda hem kendim için hemde okuyanlar için bakabilecekleri bir kaynak olması açısından bir veri bilimcinin bilmesi gereken istatistiksel konstepleri matematiğe boğmadan ve örneklerle anlatımı zenginleştirerek anlatmaya çalışacağım. Ayrıca temel istatistik dersi veya modelleme dersi alanlar için konuları daha iyi anlamak açısından ve gerçek hayatta kullanımını görmek açısından faydalı bir kaynak olabilir. Bon voyage!
- Grafik Türleri
- Örnek veri seti üzerinde grafik türleri
- Descriptive Statistics (Tanımlayıcı istatistikler)
- Olasılık Dağılımları
- Hipotez Testleri
Grafik Türleri
Veri grafikleri veriyi daha etkili anlamamızı ve dolayısıyla daha sağlam yorumlar yapabilmemizi sağlar bu yüzden herhangi bir veri bilimi projesine adım attığımızda ilk yapmamız gereken şeylerden biri de sahip olduğumuz veriyi görselleştirmektir.
Çoğu veri bilimi projesinde genellikle iki amaç için grafik kullanılır bunlardan biri özniteliğin dağılımını incelememizi sağlayan grafiklerdir. Bir diğeri ise iki veya daha fazla öznitelik arasındaki ilişkiyi incelememizi sağlayan grafiklerdir. Öncelikle bilmemiz gereken bazı grafikleri kısa cümlelerle açıklayalım sonra da bir veri seti üzerinde grafikleri inceleyelim.
Değişkenler arası ilişkiyi incelemek için bazı grafikler:
Scatter Plot: İki değişken arasındaki ilişkiyi göstermek için nokta bulutları kullanır. (x ve y değişkeni arasındaki ilişkiyi görürüz)
Line Plot: İki değişken arasındaki ilişkiyi çizgi ile gösterir. (x ve y değişkeni arasındaki ilişkiyi görürüz)
Bar Plot: Kategorik değişkenlerin sayısal değerlerini görselleştirmek için kullanılır. Örneğin kadın ve erkek sayısını içeren bir özniteliğimiz olsun. Kadın ve erkek sayısını karşılaştırmak isterken kullanılabilir.
Heatmap: Değişkenler arasındaki ilişkiyi renklerle gösteren bir matris gösterimi sunar. (Veri setindeki tüm özniteliklerin kendi aralarındaki korelasyonlarını bir grafikte inceleyebiliriz.)
Distribution(dağılım) incelemek için bazı grafikler:
Histogram: Bir değişkenin dağılımını görselleştirmek için kullanılır.
Pie Chart: Bir kategorik değişkenin oransal dağılımını göstermek için kullanılır.
Box Plot: Değişkenin merkezi eğilimini, yayılımını ve özellikle de aykırı değerlerini görselleştirmek için kullanılır.
Örnek veri seti üzerinde grafik türleri
Şimdi klasik ‘iris’ veri seti üzerinde yukarıda bahsettiğimiz grafik çeşitlerini inceleyelim. Bu veri setinde 3 farklı iris bitki türünün 50 farklı örneği ve bunların her birinin 4 farklı özelliği toplanmış amacımız ise bu özellikleri kullanarak verilen örneğin hangi bitki türüne ait olduğunu bulmak.
Özniteliklerin İsimleri:
- sepal length (cm cinsinden): Çanak yaprağı uzunluğu
- sepal width (cm cinsinden): Çanak yaprağı genişliği
- petal length (cm cinsinden): Taç yaprağı uzunluğu
- petal width (cm cinsinden): Taç yaprağı genişliği
Bitki türleri(tahminlemeye çalıştığımız hedef sınıf):
- Iris-Setosa (label değeri olarak 0)
- Iris-Versicolour (label değeri olarak 1)
- Iris-Virginica (label değeri olarak 2)
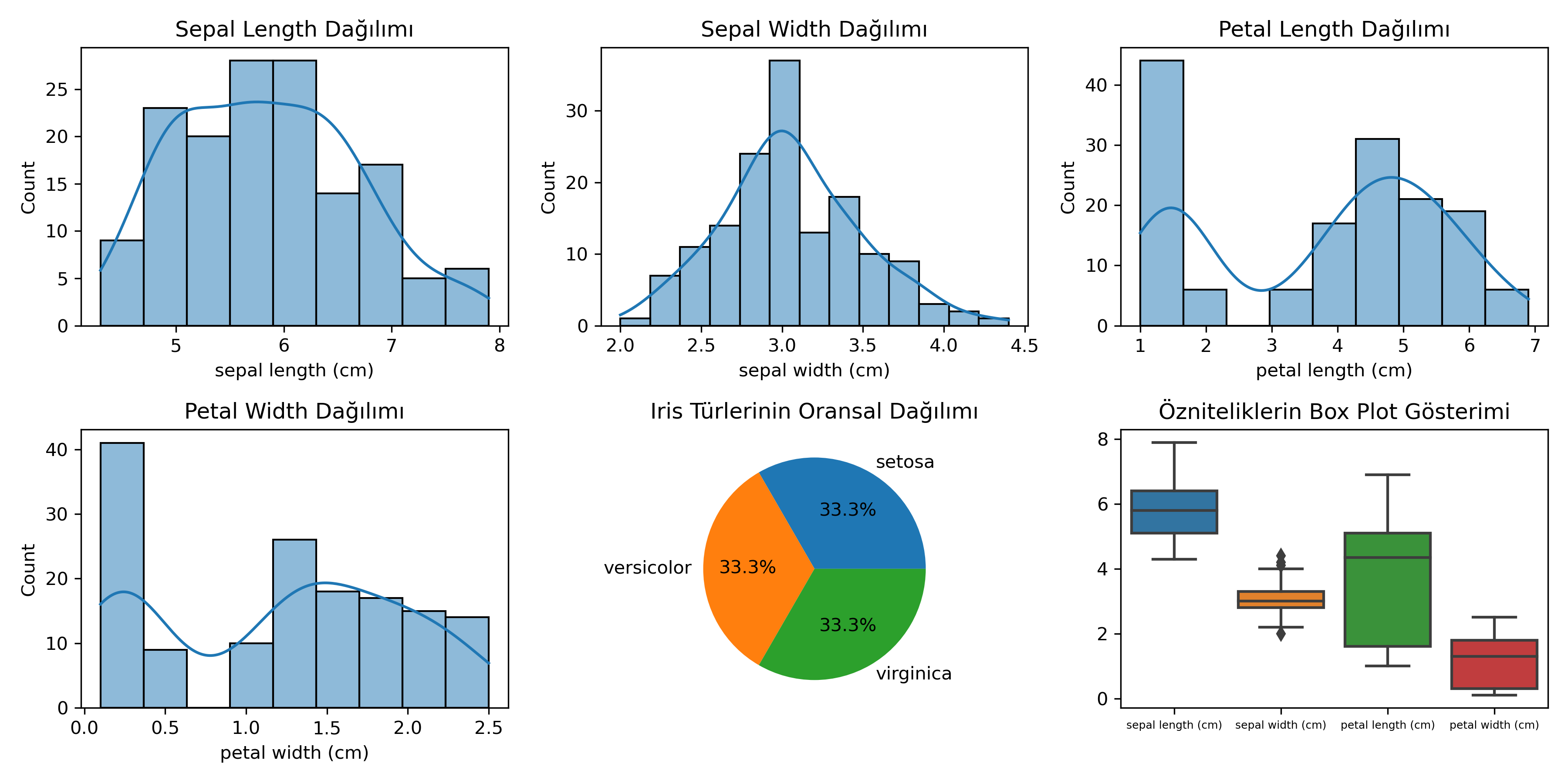
Bu altı grafikte öncelikle 4 özniteliğimiz olan sepal length, width ve petal length,width özniteliklerinin dağılımlarını görüyoruz. Bu dağılımları görmek için histogramlar kullandık x-ekseninde özniteliğin değer aralığı ve y-ekseninde ise o değer aralığında kaç tane örnek olduğunun sayısını görüyoruz. 5. grafiğimiz bir pie chart bu ise hedef olan sınıfın dağılımını bize yüzdesel olarak gösteriyor. Başta da söylediğimiz gibi 3 farklı sınıfın 50 tane örneği var yani her bir hedef sınıf %33,3 oranında veri setinde örneğe sahip. En son grafiğimiz olan 6. grafik ise bir box plot bu grafikte 4 farklı özniteliğin dağılımını kutu şeklinde görüyoruz. Kutuların arasından geçen çizgi “medyan” değerini gösteriyor. Kutunun altı ve üstü %25 ve %75 aralıktaki verileri gösteriyor. Kutunun dışına uzanan çizgilerin dışındaki değerler ise outlier(dış değer) değerleri gösteriyor. Örneğin sepal-width özelliğinin çoğu değerinin belli bir aralıkta olduğunu görüyoruz ve bu aralıkta olmayan outlierlar olduğunu görüyoruz.
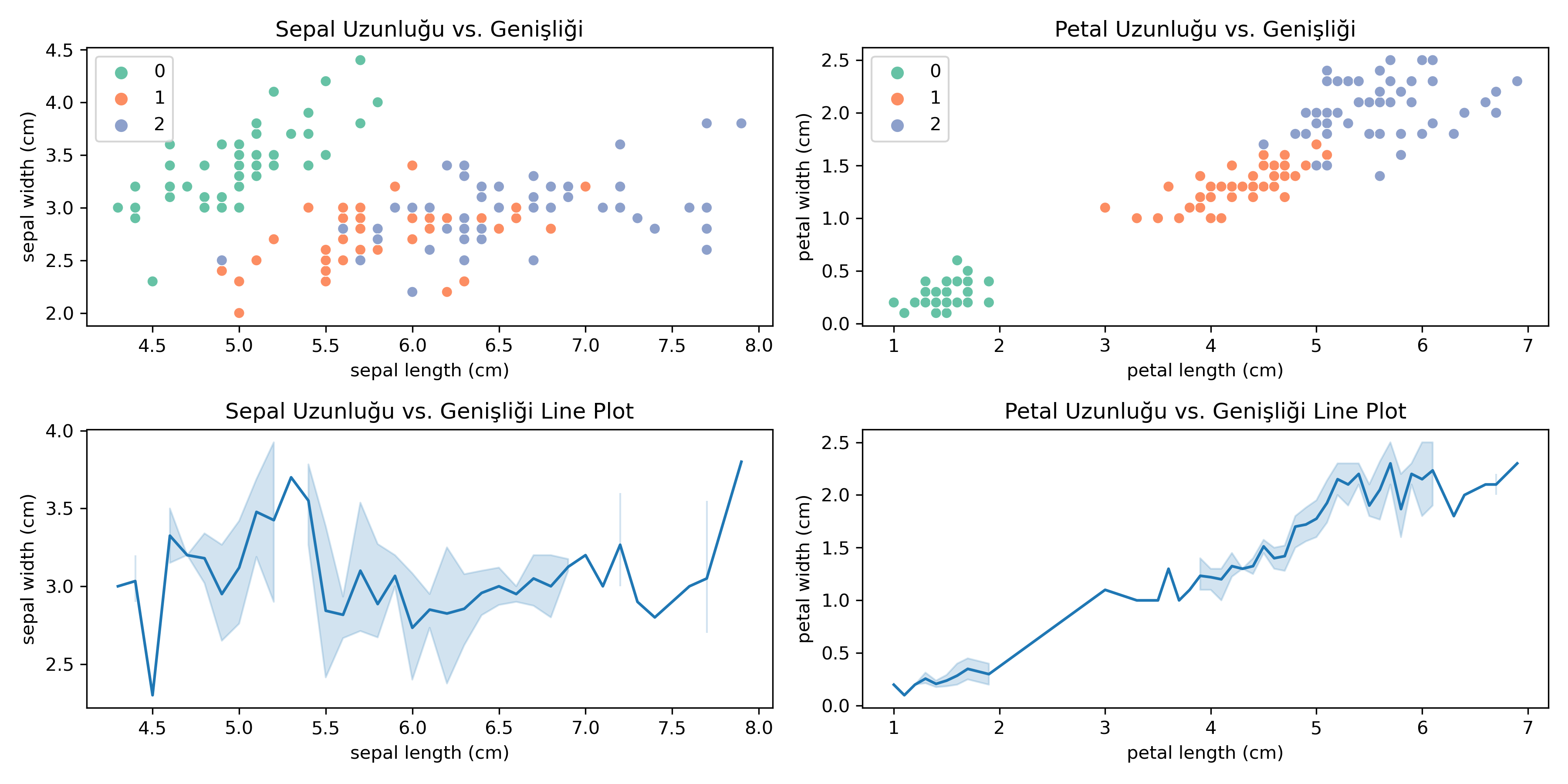
Bu dört grafikte verilerin kendi aralarındaki ilişkilerin grafikleri yer alıyor. İlk iki grafikte, sepal length vs width ve petal length vs width için scatter plot’lar görüyoruz. Her sınıf farklı renkte gösterilmiştir ve bu noktaların her biri o özniteliklerin değerlerini gösterir örneğin x-ekseninde sepal length y-ekseninde ise sepal width bulunur. Üçüncü ve dördüncü grafiklerde ise sepal length vs width ve petal length vs width için line plot’lar bulunmaktadır. Line plotlar basitçe x-ekseni artarken y-ekseninin nasıl davrandığını gösterir ancak line plotları genellikle zaman serisi verilerinde kullanmak daha doğrudur burada sadece göstermek amaçlı kullanılmıştır. Bu grafiklerde, her bir sınıfın özelliklerdeki ortalamalarının nasıl değiştiğini görebiliriz. Bu grafiklerden çıkarabileceğimiz yorumlardan biri sadece petal length ve petal width özelliklerini kullanarak bu sınıfları “lineer” olarak ayırabileceğimizdir(örneğin support vector machine modelleri ile) ancak sadece sepal length ve width özelliklerini kullanırsak bu sınıfları “lineer” olarak ayıramayız çünkü her ne kadar 0 olarak labellanan sınıf diğerlerinden lineer bir şekilde ayrılsada diğer iki sınıfın birbirinden lineer olarak ayrılamayacak kadar daha kompleks bir ilişki içerisinde olduğunu görüyoruz. Bu tarz grafiklerle öznitelikler arasındaki ilişkileri incelemek bize hangi modelleri kullanıp kullanmayacağımız hakkında bilgi verebilir.
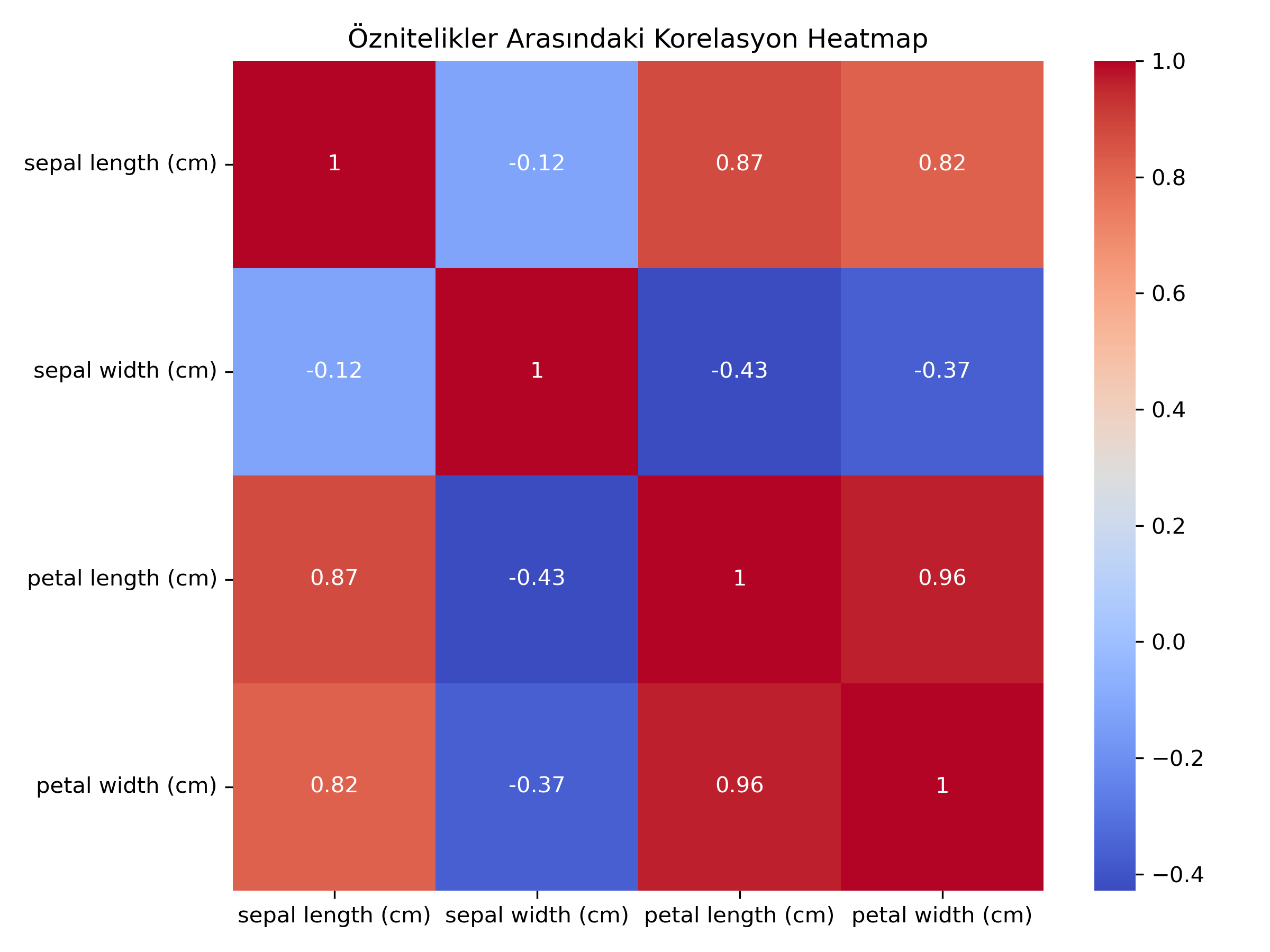
Bu grafik çeşidine heatmap denmektedir. Ve bu grafiğe bakarak hangi özelliklerin hangileriyle daha fazla korele olduklarını görebiliriz. 1 değeri tam lineer bir ilişki olduğunu gösterir ve “sıcak”lığı fazladır daha kırmızıdır kısacası -1 ise tam tersi lineer bir ilişki olduğunu gösterir yani bir değer azalırken diğerinin arttığını söyler. 0 ise aralarında bir ilişki bulunmadığını gösterir. Genellikle modeller oluştururken feature selection(öznitelik seçimi)nda bu grafikten yararlanılır. Aralarında 0.95 gibi değerlerden daha fazla (veya -0.95) korelasyon olan öznitelikler genellikle modele ekstra “bilgi” vermez. Bu nedenle öznitelik seçimi yaparken yüksek korelasyonlu özniteliklerin dikkatlice değerlendirilmesi önemlidir.
Böylece grafik çeşitleri kısmının sonuna geliyoruz. Bu “iris” verisetini daha fazla grafik çeşitleriyle incelemekten çekinmeyin. Daha fazla grafik çeşitlerine buradan ulaşabilirsiniz. Bu bölüm için yazılan Python kodu aşağıdaki gibidir.
# Kütüphaneler
from sklearn import datasets # iris verisini almak için
import matplotlib.pyplot as plt # ana grafik kütüphanesi
import seaborn as sns # matplotlib üstüne kurulan daha güzel grafikler içeren kütüphane
import pandas as pd # veriyi dataframe olarak almak için
iris = datasets.load_iris()
X = iris.data
y = iris.target
features = pd.DataFrame(X, columns=iris.feature_names)
# Özniteliklerin dağılımını incelemek için grafikler
plt.figure(figsize=(12, 6))
plt.subplot(2, 3, 1) # 2 satır 3 sütundan oluşan grafik spotları ve ilk grafik şu şekilde olsun
sns.histplot(features['sepal length (cm)'], kde=True)
plt.title('Sepal Length Dağılımı')
plt.subplot(2, 3, 2) # 2 satır 3 sütundan oluşan grafik spotları oluştur ve ikinci grafik şu şekilde olsun
sns.histplot(features['sepal width (cm)'], kde=True)
plt.title('Sepal Width Dağılımı')
plt.subplot(2, 3, 3)
sns.histplot(features['petal length (cm)'], kde=True)
plt.title('Petal Length Dağılımı')
plt.subplot(2, 3, 4)
sns.histplot(features['petal width (cm)'], kde=True)
plt.title('Petal Width Dağılımı')
plt.subplot(2, 3, 5)
sizes = features.groupby(y).size()
plt.pie(sizes, labels=iris.target_names, autopct='%1.1f%%')
plt.title('Iris Türlerinin Oransal Dağılımı')
plt.subplot(2, 3, 6)
sns.boxplot(data=features).tick_params(axis='x', labelsize=6)
plt.title('Özniteliklerin Box Plot Gösterimi')
# Değişkenler arası ilişkiyi incelemek için grafikler
plt.figure(figsize=(12, 6))
plt.subplot(2, 2, 1)
sns.scatterplot(x='sepal length (cm)', y='sepal width (cm)', data=features, hue=y, palette='Set2')
plt.title('Sepal Uzunluğu vs. Genişliği')
plt.subplot(2, 2, 2)
sns.scatterplot(x='petal length (cm)', y='petal width (cm)', data=features, hue=y, palette='Set2')
plt.title('Petal Uzunluğu vs. Genişliği')
plt.subplot(2, 2, 3)
sns.lineplot(x='sepal length (cm)', y='sepal width (cm)', data=features)
plt.title('Sepal Uzunluğu vs. Genişliği Line Plot')
plt.subplot(2, 2, 4)
sns.lineplot(x='petal length (cm)', y='petal width (cm)', data=features)
plt.title('Petal Uzunluğu vs. Genişliği Line Plot')
# Korelasyonları görmek için Heatmap
plt.figure(figsize=(8, 6))
sns.heatmap(features.corr(), annot=True, cmap='coolwarm')
plt.title('Öznitelikler Arasındaki Korelasyon Heatmap')
plt.tight_layout()
plt.show()
Descriptive Statistics (Tanımlayıcı istatistikler)
Tanımlayıcı veya betimsel istatistikler bize veri setinin karakteristiklerini sunar ve veri analizi yaparken önemli ve ilk aşamalardan birisidir. Aslında tanımlayıcı istatistikler bir nevi verinin özetidir denebilir. Bu “özet” üç kategoriden oluşur; merkezi eğilim, değişkenlik ölçüleri, dağılım. Bu kategorileri daha da açmak gerekirse :
Merkezi Eğilim Ölçüleri:
Ortalama (Mean): Veri setindeki tüm değerlerin toplamının, toplam veri sayısına bölünmesiyle elde edilen bir ölçüdür. Verinin merkezini temsil eder.
Ortanca (Median): Veri setindeki değerlerin sıralandığında ortada bulunan değerdir. Ortalamanın aksine veri setindeki outlierlardan etkilenmez dolayısıyla veri setinde dış değerler çok iken verinin merkezini daha iyi temsil eden bir ölçüdür.
Mod ya da Tepe Değer (Mode): Veri setinde en sık tekrar eden değeri ifade eder. Verilen veri kategorik ise verinin merkezini daha iyi temsil eder.
Değişkenlik Ölçüleri:
Varyans (Variance): Veri noktalarının ortalama etrafındaki dağılım derecesini ölçer. Daha büyük bir varyans, veri noktalarının ortalama etrafında daha geniş bir dağılıma sahip olduğunu gösterir dolayısıyla verilerin daha dağınık olduğunu söyler. Formülü aşağıdaki gibidir. (N toplam veri sayısıdır, $x_i$ her bir veri noktasını $\bar{x}$ ise verinin ortalamasını gösterir)
\[\sigma^2 = \frac{1}{N} \sum_{i=1}^{N} (x_i - \bar{x})^2\]Standart Sapma (Standard Deviation): Varyansın kareköküdür, dolayısıyla aykırı değerlere karşı daha dirençlidir ve daha küçük bir değer olduğu için standart sapmaları karşılaştırmak daha doğal gelir.
Kovaryans (Covariance): İki özniteliğin veya değer kümesinin birlikte ne kadar değiştiklerinin ölçüsüdür. Örneğin x1 değişkenin büyük olduğu yerlerde x2 değişkenide büyük bir değer alıyorsa kovaryansları pozitif olur tam tersi olan birinin daha küçük olduğu yerlerde diğeri de daha küçük ise kovaryansları negatif olur. Aynı zamanda her bir özniteliğin birbiriyle kovaryansının değerinin olduğu kovaryans matrisi oluşturulabilir bu matris PCA yaparkende kullanılır. PCA yöntemiyle örneğin 50 tane özniteliğin olduğu bir veri setini 2 veya 3 “en önemli” (burda en önemliler varyans eşiğiyle belirlenir) özniteliğe kadar indirebilir ve bu sayede veriyi görselleştirebiliriz. Kovaryansın formülü aşağıdaki gibidir
\[\sigma(x, y) = \frac{1}{n - 1} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})\]Çeyrekler Açıklığı (Interquartile Range - IQR): Aykırı değer olarak bahsettiğimiz outlierların bulunmasında yardımcı olur. Veri setinin 3. çeyrekliği -3. çeyreklik demek verilerimizin kaçı %75lik dilime giriyor ? sorusunu cevaplar örneğin medyan ise verilerimizin kaçı %50ye giriyor sorusunu cevaplar- ile 1.çeyrekliğinin(%25lik kısım) farkıdır. Bulunan çeyrekler açıklığına IQR dersek ve Q1 birinci çeyreğin değeri, Q3 ise üçüncü çeyreğin değeri dersek. (Q1 - 1.5IQR, Q3 + 1.5IQR) aralığının dışında kalan değerler genellikle “aykırı değer” kabul edilir.
Aralık (Range): Veri setindeki en büyük ve en küçük değer arasındaki farktır. Ancak bu değer aykırı değerlerden etkilenebilir. Genellikle doğrudan verideki maksimum ve minimum değerler bakmak veriyi anlamak adına daha sağlıklı olabilir.
Dağılım:
Histogramlar: Veri setini belirli aralıklara böler ve her aralıktaki veri noktalarının sayısını gösterir. Veri setinin dağılımını görselleştirmek için sıklıkla kullanılır. Yukarıda “Iris” veri seti üzerinde bir örneğini görmüştük.
Frekans Tabloları: Her bir değerin veri setinde kaç kez tekrarlandığını gösterir. Kategorik veriler için frekans tabloları, veri setinin sıklıkla karşılaşılan değerlerini belirlemek için kullanışlıdır.
Olasılık Yoğunluk Fonksiyonları (PDF): Her bir değerin olasılığını belirtir ve genellikle sürekli değişkenlerin dağılımını tanımlar.
Kümülatif Dağılım Fonksiyonları (CDF): Belirli bir değerin o değere kadar olan kümülatif olasılığını gösterir. Veri setinin genel dağılımını anlamak için kullanılır.
Dağılımlara sonraki bölümlerde ekstra daha detaylı olarak bakacağız.
Bir veri setini pandas dataframe olarak yükledikten sonra veri setinin temel istatistiklerine kolayca aşağıdaki gibi bakabilirsiniz.
df = pd.DataFrame(data) # veriyi yüklediniz veya oluşturdunuz diyelim
print(df.describe()) # verinin temel istatistiklerini bastırır.
Örneğin aşağıda describe() metodunun “Iris” veri setindeki öznitelikler üzerindeki sonucu verilmiştir. Bu temel istatistiklerle veriyi daha iyi anlayabiliriz.

Olasılık Dağılımları
Olasılık dağılımları, rassal değişkenlerin farklı değerlerinin olasılıklarını temsil eden matematiksel fonksiyonlardır. Örneğin, normal dağılım, birçok doğal olayın (bir ortamdaki kişilerin boy uzunluğu, IQ skoru, belirli bir tür çam ağacının gövde çapı gibi) dağılımını iyi bir şekilde modelleyebilir.
Her dağılımın olduğu gibi yukarıdada bahsettiğimiz gibi normal dağılımın bir olasılık yoğunluk fonksiyonu (PDF) vardır. Bu fonksiyon, herhangi bir değerin olasılığını hesaplamak için kullanılabilir. Ayrıca, normal dağılımın ortalama ve standart sapması gibi belirli parametreleri vardır; bu parametreler dağılımın şeklini ve merkezini tanımlar.
Bu dağılımlar, veri setinin belirli özelliklerini daha iyi anlamamıza ve gelecekteki olayları tahmin etmemize yardımcı olabilir. Ayrıca normal dağılım gibi bazı dağılımlar bazı modeller için (örneğin genellikle naive bayes) daha iyi sonuç verir.
Şimdi veri bilimi için bazı önemli istatistiksel dağılımlara göz atalım ve nerelerde karşımıza çıkar, ne özellikleri vardır, ne işimize yarar öğrenelim.
Bernoulli Dağılımı:
En basit dağılımlardan biridir. Tek bir denemede iki olası sonuçlu olayları modellemek için kullanılır. Örneğin, bir madeni para atıldığında yazı gelme olasılığını modellemek için kullanılabilir.
Uniform Dağılımı:
Belirli bir aralıkta herhangi bir değerin eşit olasılıkla ortaya çıkabileceğini ifade eden bir dağılımdır. Örneğin, bir zarın atılması gibi her bir sonucun eşit olasılığa sahip olduğu durumlarda kullanılır.
Binomial Dağılım:
Belirli bir deneme sayısında ardışık Bernoulli denemelerinin sayısını modellemek için kullanılır. Binom dağılımı, n bağımsız ve aynı dağılıma sahip Bernoulli denemesinin sonuçlarını modellemek için kullanılır. Örneğin, bir madeni paranın 10 kez atılması ve tura gelme sayısının modellemesi için kullanılabilir.
Normal(Gaussian) Dağılım:
Doğal olaylarda ve ölçümlerinde(dolayısıyla veri setlerinde) sıklıkla gözlemlenen, simetrik ve çan şeklinde bir dağılım modelidir. Ortalama ve standart sapma ile tanımlanır.
Exponential(Üstel) Dağılım:
Bağımsız olarak gerçekleşen olayların arasındaki sürenin dağılımını modelleyen bir sürekli olasılık dağılımıdır. Belirli bir aralıkta bir olayın gerçekleşmesi arasındaki sürenin olasılığını modellemek için kullanılır. Örneğin bir fabrikaya gelen ürünlerin arasındaki zamanı modellemek için kullanılabilir.
Poisson Dağılımı:
Belirli bir zaman aralığında olayların ortaya çıkma olasılığını modelleyen bir dağılımdır. Olayların oluşma sayısını tahmin etmek ve analiz etmek için kullanılır. Örneğin bir restorana bir gün içerisinde gelen toplam müşteri sayısını modellemek için kullanılabilir.
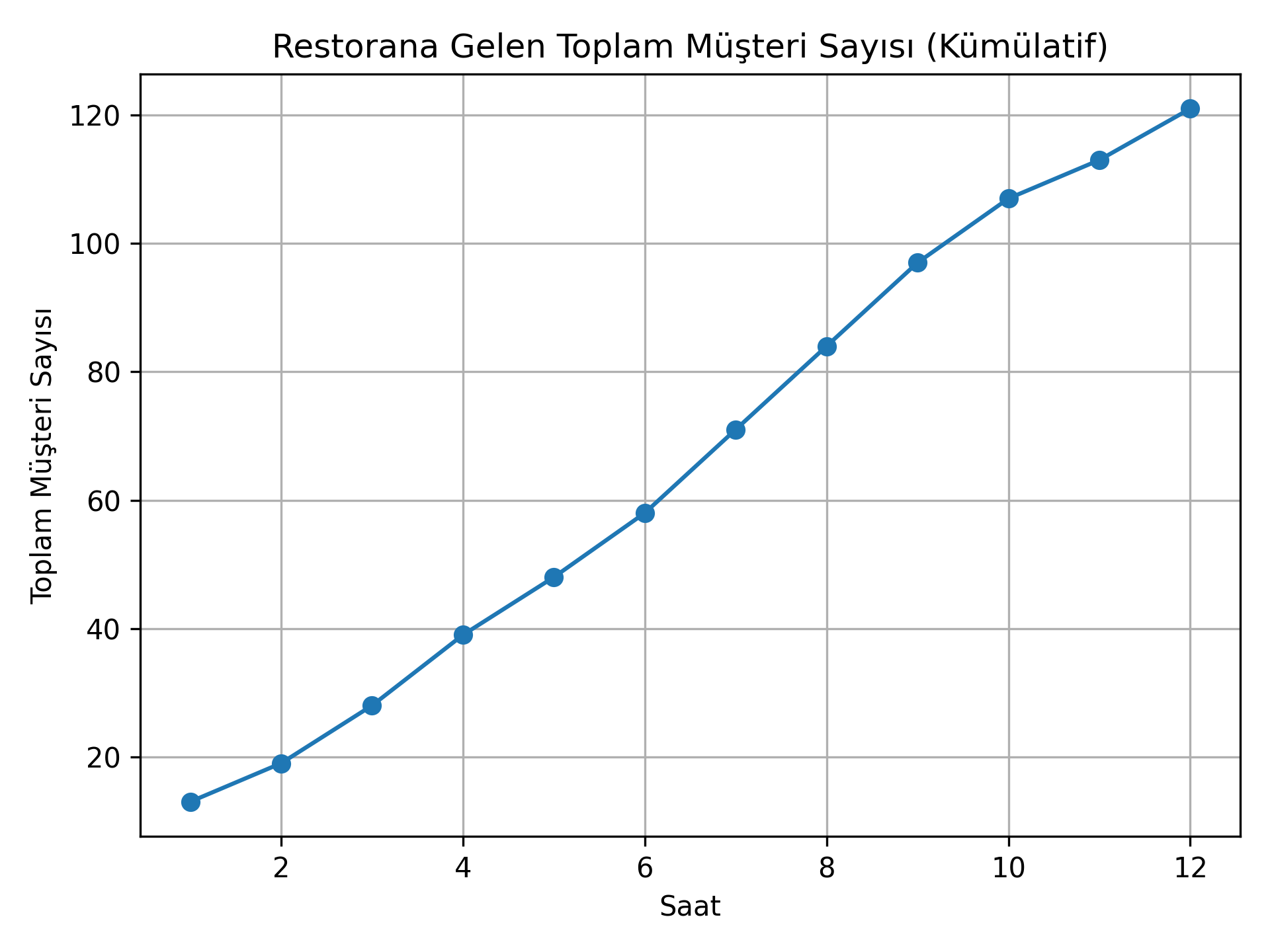
Belirli bir olayın dağılımı hakkında gözlem sonucu elinizde parametreler varsa ve hangi dağılıma uyacağını biliyorsanız o olayı dağılımsal olarak modelleyebilirsiniz. Topladığınız veri üzerinde bir yapay öğrenme(ya da bilinen adıyla makine öğrenimi) modeli eğitmek yerine dağılımsal modeli kullanarak gelecekteki olayların tahmin edebilir veya belirli durumların olma olasılığını hesaplayabilirsiniz. Bu analizler, veri bilimi, istatistik ve genel olarak karar verme süreçlerinde faydalıdır ve bir yapay öğrenme modeli geliştirip eğitmekten çok daha kolaydır. Pythonda NumPy Random Generator ile parametrelerini belirlediğiniz bir dağılımı rastgele oluşturabilirsiniz. Aşağıda örnek olması açısında saatte ortalama 10 müşteri gelen bir restoranın saatler içindeki müşteri sayısı Poisson dağılımıyla olarak modellenmiştir.
import numpy as np
import matplotlib.pyplot as plt
hours_open = 12 # restoranın açık olduğu saat sayısı
mean_customers_per_hour = 10 # her saat için ortalama müşteri sayısı
# Oluşan rastgeleliği deterministik yapmak için rassal sayı "üreteci".
rng = np.random.default_rng(42)
hourly_customers = rng.poisson(mean_customers_per_hour, size=hours_open)
total_customers = np.sum(hourly_customers)
hours = np.arange(1, hours_open + 1)
customer_count = np.cumsum(hourly_customers)
plt.plot(hours, customer_count, marker='o')
plt.title('Restorana Gelen Toplam Müşteri Sayısı (Kümülatif)')
plt.xlabel('Saat')
plt.ylabel('Toplam Müşteri Sayısı')
plt.grid(True)
plt.show()
Hipotez Testleri
Hipotez anakütlenin durumu hakkında öne sürülen “iddia”lardır. Bir hipotezkl testi ise belirli bir örneklem verisine dayanarak bir hipotezin doğruluğunu test etmeyi amaçlar. İstatistiksel bir testte, genellikle iki hipotez vardır: null hipotez($H_0$) ve alternatif hipotez($H_1$ veya $H_a$). Null hipotez, genellikle varsayılan durumu ifade ederken, alternatif hipotez ise null hipotezi reddetmek için test edilen iddiayı ifade eder.
Anlamlılık Seviyesi ($\alpha$): Null hipotezin reddedilmesi için kabul edilebilir en yüksek hata olasılığını belirtir. Araştırmadan araştırmaya değişmekle beraber yaygın olarak anlamlılık seviyeleri 0.05 ve 0.01’dir nadirende olsa bazı durumlarda 0.1 olarak da seçilebilir.
p-değeri: null hipotez testi bağlamında istatistiksel anlamlılığı ölçmek için kullanılır. Yani p-değeri, null hipotezinin doğru olduğu varsayımının ne kadar inandırıcı olduğunu ifade eder. Test sonucu ortaya çıkan p-değeri anlamlılık seviyesi olan $\alpha$ ile karşılaştırılır. Eğer p-değeri, anlamlılık seviyesinden (genellikle 0.05) daha düşükse, bu null hipotezinin reddedilmesi gerektiği anlamına gelir. Bu durumda, verilerin null hipotezi desteklemediği ve alternatif hipoteze daha yakın olduğu söylenebilir. Ancak, p-değeri anlamlılık seviyesinden büyükse, null hipotezi reddedilemez ve veriler null hipotezle uyumlu olarak değerlendirilir.
Birçok hipotez testi tipi bulunmaktadır bu blog yazısında hepsine değinemeyeceğimizden dolayı buraya problem tipinize göre SciPy’da implemente edilmiş bir test bulabileceğiniz faydalı bir dokümentasyon bırakıyorum. Aşağıda ise bazı hipotez testleri ve kullanımları verilmiştir.
Eğer bir örneklemin ortalaması ile teorik bir değer arasında anlamlı bir fark olup olmadığını test etmek istiyorsanız, t-testi gibi parametrik bir test kullanabilirsiniz. Örneğin, iki grup arasında ortalama bir farkın olup olmadığını test etmek için t-testi kullanabilirsiniz.
Bununla birlikte, varyanslar hakkında belirli bir önerme test etmek istiyorsanız, F-testi gibi bir test kullanabilirsiniz. Örneğin, iki grup arasındaki varyansların eşit olup olmadığını test etmek için F-testi kullanılabilir.
Bir kategorik değişkenin oranlarını karşılaştırmak için kullanabileceğiniz bir başka test ise ki-kare testidir. Örneğin, hangi reklamın daha efektif olduğunu ölçmek için bir grup insanın iki farklı reklam arasındaki tercihini karşılaştırabilirsiniz. (Bu oldukça kullanılan A/B testine bir örnektir.)
Eğer bir grup verinin dağılımı normal olup olmadığını test etmek istiyorsanız, Shapiro-Wilk testi gibi bir normalite testi kullanılabilir.
Aşağıda örnek olması açısından t-testi kodu verilmiştir.
import numpy as np
from scipy.stats import ttest_ind
rng = np.random.default_rng(42)
# boy ortalaması 170 olan bir örneklem grubu (A anakütlesinin)
group_a_heights = rng.normal(loc=170, scale=5, size=100)
# boy ortalaması 171 olan diğer bir örneklem grubu (B anakütlesinin)
group_b_heights = rng.normal(loc=171, scale=5, size=100)
# varyansı aynı olan bağımsız iki popülasyon arasında t-testi
t_statistic, p_value = ttest_ind(group_a_heights, group_b_heights)
# p-degeri ile karşılaştıracağımız alpha değeri. Genellikle 0.01 veya 0.05 seçilir
alpha = 0.05
print("T-Statistic:", t_statistic)
print("P-Value:", p_value)
if p_value < alpha: print("Reject the null hypothesis. There is a significant difference in average height between Group A and Group B.")
else: print("Fail to reject the null hypothesis. There is no significant difference in average height between Group A and Group B.")
T-Statistic: -1.9169951303944577
P-Value: 0.05667816873538445
Fail to reject the null hypothesis. There is no significant difference in average height between Group A and Group B.