Merhabalar, yeni blog yazıma hoşgeldiniz. Bugün hiperparametre optimizasyonu üzerine konuşacağız, umarım okuyanlara faydalı bir yazı olur!

  1. Hiperparametre vs parametre aralarındaki fark nedir ?
  2. Hiperparametre optimizasyonu yöntemleri
    1. Grid Search
    2. Random Serch
    3. Grid Search vs Random Serch
    4. Bayesian Optimization (Bayes optimizasyonu)
  3. Iris Veri seti üzerinde örnek bir uygulama

Hiperparametre vs parametre aralarındaki fark nedir ?

Aradaki farkı öğrenmek için iki farklı regresyon modelini inceleyelim.

Parametreler modelin veriden çıkardığı bilgiler sonucu güncellenen değerlerdir yani parametreleri algoritmanın kendisi öğrenir. Örneğin basit bir doğrusal regresyon denklemi

\[y = \beta_0 + \beta_1x\]

şeklinde gösterilebilir. Bu denklemde $x$ bağımsız değişken $y$ tahmin etmeye çalıştığımız bağımlı değişken, $\beta_0$ ve $\beta_1$ modelin optimize edeceği parametrelerdir.Verilen verilere göre bir loss function eşliğinde doğrusal regresyon algoritması bu parametreleri optimize eder.

Hiperparametreler model eğitilmeye başlamadan önce bizim tarafımızdan değeri belirlenir ve modelin veriyi nasıl öğreneceğini belirler. Örneğin yukarıda bahsettiğimiz basit doğrusal regresyon modelinin daha kapsamlı öğrenmesini sağlamak için ridge regresyonu adı verilen başka bir regresyon algoritması kullanılabilir. Bu regresyonda ise kontrol etmemiz gereken bir hiperparametre olan lambda bulunur. Varsayalımki basit doğrusal regresyon modelimizin optimize etmeye çalıştığı loss function En Küçük Kareler fonksiyonu olsun

\[L = \sum_{i=1}^n(y_i - \hat{y}_i)^2\]

bu denklemde n toplam veri noktalarının sayısı. $\hat{y}_i$ modelin tahmin ettiği y değeridir. $y_i$ ise gerçekte olan y değeridir. Modelimiz eğitildiği veri üzerinde gördüğü her bir değeri tahmin edecek ve tahmin sonucu bu loss functiondaki “skoruna” bakacaktır ve kendisini buna göre optimize edecektir. Yani yapmaya çalışacağı şey En Küçük Kareler fonksiyonunda 0’a ulaşmaktır. Ancak bunu yaparken modelimiz overfitting denilen bir sorunla karşılaşabilir bu da modelin eğittimiz veriyi “ezberlemesi” ve kendisini kapsamlı bir tahmin edici yapamamasıdır.Bunun önüne geçmek için ridge regresyonunda bir penalty(ceza) terimi bulunur.

\[L = \sum_{i=1}^n(y_i - \hat{y}_i)^2 + \lambda \sum_{j=1}^p(W_j)^2\]

bu loss function da başındaki En Küçük Kareler dışında \(\color{red}\lambda \sum_{j=1}^{p} (W_j)^2\) terimi bulunur buna L2 cezası denir ve modeldeki tüm katsayıların(örneğin basit doğrusal regresyonda $\beta_1$ bir katsayıydı) toplamının lambda değeri ile çarpılmasıdır. Burada lambda bizim kontrol ettiğimiz bir hiperparametredir ve modelin nasıl öğreneceğini belirler.

Hiperparametre optimizasyonu yöntemleri

Bu blog yazısında 3 farklı hiperparametre optimizasyon yönteminden bahsedeceğiz.

  1. Grid Search
  2. Random Search
  3. Bayesian Optimization

Hiperparametrelerin belirli bir değer aralığında tüm kombinasyonlarının denenerek en iyi kombinasyonun bulunmasını sağlayan bir yöntemdir. Bu yöntem, kapsamlıdır ancak zaman alıcıdır.

Random Serch

Hiperparametrelerin belirli bir değer aralığında tüm kombinasyonlarının denenmesi yerine verilen sayı kadar rastgele kombinasyonları değerlendirir ve en iyisini seçer. Bu yöntem daha az kapsamlıdır ancak modelin fazla hiperparametresi veya hiperparametrelerin alabileceği değer aralığı fazlaysa grid searchten çok daha hızlıdır.

Grid Search vs Random Serch

Örneğin bir Decision Tree(Karar Ağacı) algoritmasının 4 tane hiperparametresini optimize etmek istiyoruz ve aşağıdaki belirli değerlerin iyi olabileceğini düşünüyoruz.

‘n_estimators’: [100, 200, 300, 400]
‘max_depth’: [None, 5, 10, 15, 20]
‘min_samples_split’: [2, 5, 10]
‘min_samples_leaf’: [1, 2, 4]

Bu değerler üzerine Grid Search yaparsak Grid Search’ün deneyeceği 4x5x3x3’ten toplam 180 tane kombinasyon vardır ve eklenen her bir hiperparametre değeri başına bu sayının çok daha fazla büyüyeceğini göz önüne alalım. Tüm kombinasyonları denemek yerine Random Search ile örneğin 25 tane kombinasyonu deneyebiliriz. Bu sayede zamandan ve hesaplama gücünden kazanırız ancak en iyi hiperparametre kombinasyonunu yakalayamayabiliriz.

Bayesian Optimization (Bayes optimizasyonu)

Bayes optimizasyonu tanım olarak kara kutu fonksiyonların global optimizasyonu için kullanılan bir yöntemdir yani verilen fonksiyonun iç yapısı hakkında bilgi sahibi olmadan yalnızca giriş-çıkış ilişkisine dayanarak en iyi sonucu bulmaya çalışır. Örneğin makine öğrenmesiyle sınıflandırma yapıyoruz diyelim, girdilerimiz hiperparametreler ve çıktılarımız modelin sonuçlarını değerlendiren “accuracy” olsun. Bayes optimizasyonu, bu hiperparametre kombinasyonlarını kullanarak modelin performansını değerlendirir ve daha sonra bu performansı eniyilemek(accuracy’i arttırmak için) için yeni hiperparametre kombinasyonları önerir bu öneriler Grid Search ve Random Searchten farklı olarak önceki denemelerden elde edilen sonuçlara dayanır. Yani bayes optimizasyonu her bir denemeden sonra hiperparametre değerlerinin performansını modelleyen bir olasılık dağılımı oluşturur ve bu dağılımı kullanarak en iyi olabilecek hiperparametre değerlerini belirler ve bunları kullanarak devam eder. Bu yöntemin avantajı daha az denemeyle daha başarılı sonuçlar ortaya çıkarabilmesidir ancak dezavantajı da önceki denemelere bakıp kendisine yön verdiğinden dolayı en başta verdiğimiz hiperparametre değerlerinin ve aralığının sağlam olması gerekir.

Iris Veri seti üzerinde örnek bir uygulama

Blogun bu kısmında klasik iris veri seti üzerinde gördüğümüz bu üç farklı yöntemi deneyeceğiz. sklearn ve skopt paketlerini kullanacağız. Başlamadan önce bu paketlerinde uyguladığı üzere neden cross-validation ile hiperparametre optimizasyonu yaptığımızın üstünden geçmek istiyorum.

Aşağıdaki resimde 5 katlı cross validation’nın şeması bulunmaktadır.

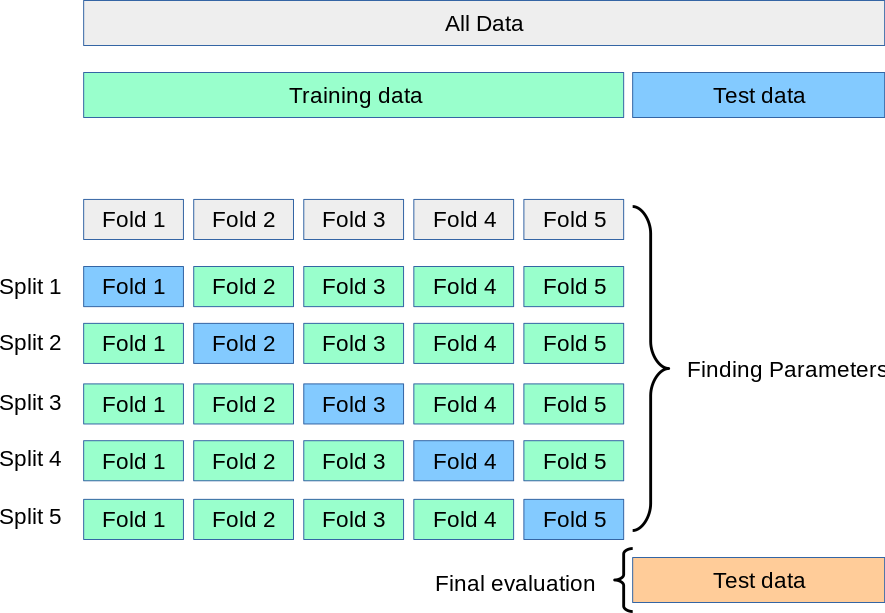
Veri seti, 5 alt kümeye (katlara) bölünür. Her bir katlama sırayla test için ayrılırken diğer katlamalar eğitim için kullanılır. Bu işlem 5 kez tekrarlanır ve her seferinde farklı bir katlama test için ayrılır. Sonuçlar ortalaması alınarak genel model performansı hesaplanır. Cross validation, modelin overfitting yapma olasılığını azaltır ve hiperparametre optimizasyonunda daha güvenilir sonuçlar elde etmemizi sağlar. Bu nedenle, hiperparametre optimizasyonu yaparken cross validation kullanmak önemlidir.

Hiperparametre optimizasyonu yaparken model hiperparametrelerini test verisine göre ayarlamamalıdır. Yoksa model test verisini ezberler ve hiperparametrelerini test verisine göre ayarlar bu yüzden yeni gelen verilere karşı iyi performans veremez
Cross validation yapmak yerine veri seti train, validation ve test diye ayırılıp. En iyi hiperparametre araması yapılırken hiperparametreler validation kümesine göre seçilebilir. Buda uygulanabilir bir yoldur ancak veri sayımız azsa cross validation yapmak daha iyi olacaktır.

Artık kodlamaya geçelim. (Kodların olduğu notebooka buradan ulaşılabilir)

Öncelikle gerekli importları yapalım ve veri setimizi yükleyelim.

import numpy as np
import pandas as pd

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, GridSearchCV, RandomizedSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import GradientBoostingClassifier
from skopt import BayesSearchCV
from skopt.space import Integer, Real

X, y = load_iris(return_X_y=True)
X.shape, y.shape

((150, 4), (150,))

Başlamadan veriyi train ve test diye ayırıp normalize edelim.

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)

sc = StandardScaler()

# veri normalleştirilirken test datası görülmemelidir(fit_transform yerine sadece transform)
# yoksa bilgi sızışı olur buda overfittinge sebebiyet verir
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

Modeli oluşturalım ve hiperparametre optimizasyonu için denenecek hiperparametrelerin havuzunu hazırlayalım. Grid Search’ün beklenebilir bir sürede çalışabilmesi için daha az parametre denemeliyiz. Random Search’e kıyasla böyle bir hesaplama süresi dezavantajı vardır.

gbc = GradientBoostingClassifier(random_state=42)

grid_param_grid = {
    'learning_rate': [0.001, 0.01, 0.1],
    'n_estimators': [50, 100, 300],
    'subsample': [0.5, 1],
    'max_depth': [2, 3]
}

Grid Search ile arama yapalım. (Toplamda 36 hiperparametre kombinasyonu denemesi yapacak)

%%time
grid_search = GridSearchCV(gbc, grid_param_grid, scoring='accuracy', cv=3, n_jobs=-1)
grid_search.fit(X_train, y_train)
print("Grid Search - En iyi parametreler:", grid_search.best_params_)
print("Grid Search - En iyi skor:", grid_search.best_score_)

Grid Search - En iyi parametreler: {'learning_rate': 0.1, 'max_depth': 2, 'n_estimators': 100, 'subsample': 0.5}
Grid Search - En iyi skor: 0.9396910279263221
CPU times: user 977 ms, sys: 168 ms, total: 1.15 s
Wall time: 52.3 s

Şimdi modelin görmediği test verisi üzerinde bu parametrelerle modelin skoruna bakalım.

print(grid_search.score(X_test, y_test))

0.96

Şimdi random search ile aynı işlemi daha büyük bir havuz üzerinde yapacağız ancak adillik olsun diye deneme sayısını tekrardan 36’ya eşitleyeceğiz :)

random_param_grid = {
    'learning_rate': [0.001, 0.01, 0.1, 0.5, 1],
    'n_estimators': [50, 100, 300, 500, 700],
    'subsample': [0.1, 0.3, 0.5, 0.7, 0.9, 1.0],
    'max_depth': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
}

%%time
random_search = RandomizedSearchCV(gbc, random_param_grid, scoring='accuracy', n_iter=36, cv=3, n_jobs=-1)
random_search.fit(X_train, y_train)
print("Random Search - En iyi parametreler:", random_search.best_params_)
print("Random Search - En iyi skor:", random_search.best_score_)

Random Search - En iyi parametreler: {'subsample': 0.3, 'n_estimators': 50, 'max_depth': 8, 'learning_rate': 0.01}
Random Search - En iyi skor: 0.9396910279263221
CPU times: user 1.13 s, sys: 211 ms, total: 1.34 s
Wall time: 1min 21s

Test verisi üzerinde Random Search sonucuna bakalım.

print(random_search.score(X_test, y_test))

0.98

Şimdi ise Bayes Optimizasyonu için aynı işlemleri yapacağız ancak elle kodlanmış sayılar yerine Bayes Optimizasyonunda bir dağılım üzerinde arama yapmak daha mantıklıdır

bayes_param_grid = {
    'learning_rate': Real(0.001, 1.0, 'log-uniform'),
    'n_estimators': Integer(50, 1000),
    'subsample': Real(0.1, 1.0, 'uniform'),  
    'max_depth': Integer(1, 10)
}
# Bu kod bayes searchte versiyon uyuşmazlığından dolayı oluşan bir deprecation hatası nedeniyle yazılmıştır
np.int = int

%%time
bayesopt_search = BayesSearchCV(gbc, bayes_param_grid, n_iter=36, scoring='accuracy', cv=3, n_jobs=-1)
bayesopt_search.fit(X_train, y_train)
print("Bayes Optimization - En iyi parametreler:", bayesopt_search.best_params_)
print("Bayes Optimization - En iyi skor:", bayesopt_search.best_score_)

Bayes Optimization - En iyi parametreler: OrderedDict([('learning_rate', 0.07693711544997084), ('max_depth', 3), ('n_estimators', 223), ('subsample',  0.17623827669841063)])
Bayes Optimization - En iyi skor: 0.9396910279263221
CPU times: user 56.5 s, sys: 28.6 s, total: 1min 25s
Wall time: 3min 36s

Test verisi üzerinde Bayesian Optimization Search’ün sonucuna bakalım.

print(bayesopt_search.score(X_test, y_test))

0.98

BayesSearch RandomSearch’e göre daha havalı hiperparametre değerleri verse de test sonucumuz aynı çıktı ve bu örnek koddan sonra bir blogun daha sonuna geldik. Umarım okuyanlara faydalı olmuştur. Görüşmek üzere!